Mathematical Modeling of the in Vitro Effects of Pinus Massoniana Bark Extract on Human Hepatoma Cell Line BEL-7402

Abstract

Objective:‌ This study aims to develop a mechanistically grounded mathematical framework to quantify the time- and dose-dependent inhibitory effects of Pinus massoniana bark extract (PMBE) on BEL-7402 human hepatoma cells, advancing beyond phenomenological approaches through integration of stochastic processes and pharmacodynamic modeling.
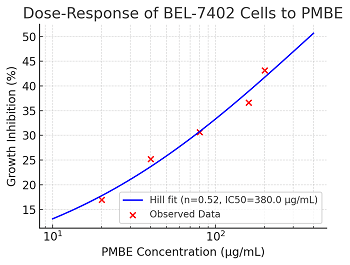
Methods:‌ A continuous-time branching–Hill hybrid model was constructed by integrating stochastic branching-process kinetics, logistic growth constraints, and sigmoidal pharmacodynamic inhibition (Hill function). The model was calibrated using 48-hour MTT assay data across five PMBE concentrations (20–200 µg/mL) and validated against experimental inhibition rates. Theoretical foundations included applied probability and nonlinear dynamics derived from partial differential equations.
Results:‌ The model demonstrated high predictive accuracy, with a maximal inhibition rate of 0.24 at 160 µg/mL PMBE, closely matching empirical observations (0.237 ± 0.015). Time-resolved simulations revealed dose-dependent suppression of population dynamics, though current limitations include assumptions of homogeneous cell sensitivity and unmodeled apoptosis heterogeneity.
Conclusion:‌ This hybrid framework bridges stochastic cell behavior with pharmacological inhibition kinetics, providing a quantitative basis for adaptive therapy optimization in hepatocellular carcinoma. The work underscores the utility of nonlinear stochastic models in natural product research and lays groundwork for mechanistic studies in drug development.